杜庆华院士诞辰一百周年之际,我的导师姚振汉教授要求我写一篇纪念短文。尽管我做杜先生倡导的边界元法已有二十多年,可是与杜先生的接触不多,所以打算写写我与边界元法的渊源以及在边界元研究中的体会,以此来纪念杜先生。我与边界元法的缘分可追溯到八十年代末,那时我在西安交通大学念本科。由于杜先生的倡导和扶持,西交大有许多老师在做边界元法,包括楼志文、乐美峰以及当时的系主任嵇醒等。当时在本科课程里有边界元法的简介,所以我从本科起就知道了杜先生的名字,印象中是一位高山仰止的大人物。记得我那时就被边界积分方程的优美所吸引,产生了几点幼稚的想法,写了一个小短文,通过我的本科毕业设计指导老师李中华教授给乐美峰教授看了,他还以为是研究生写的。由于种种原因,本科毕业后没有继续读研,而选择去企业工作,这样我与边界元法的缘分就中断了。
到九十年代末,我投到姚老师门下做边界元研究,亲眼看到我仰慕的大英雄时,杜先生已经八十岁了。虽然有点老态龙钟,但大学者的风范犹存。有一次杜先生去上海交通大学访问,姚老师指派我陪同,算是有了机会与杜先生第一次亲密接触,发现杜先生原来是一位和蔼可亲的慈祥老人。后来我去日本做博士后研究,杜先生为我写了推荐信,还特意跟我介绍了我在日本的合作者田中教授的性格,以及在日本生活的注意事项。至今想来,仍心存感念。
在杜先生主导国内边界元法研究的一二十年间,可以说是边界元法研究最辉煌的时期,我却错过了。拉格朗日遗憾没有生在牛顿的时代;玄奘取经路上经过佛祖的故乡,看到佛法的衰微而生荒凉之叹。我生在正确的年代,却错过了极好的机缘。当我十年后返回高校学习研究边界元法,边界元法就开始衰落了。由于姚老师的提倡,快速多极算法在国内曾掀起一阵热潮。但是整个大背景就要落幕,这一热潮恐怕也只能算是最后的一点"余辉"罢。当我从日本回国做教授,专门从事边界元法软件研发,边界元法更是日薄西山,基本上被边缘化了。获得研究经费愈加困难,文章不易发表。国际上唯一的边界元杂志(EABE)为了生存,也要向无网格法靠拢。即便这样,它在国内的杂志等级划分中也只排在三区之列。
我始终相信边界元法是一个科学的方法,有限元法是一种工程的方法,而科学的方法应该是工程问题的最终解决方案。工程方法容易实现,效率高,因为它的计算模型对真实结构做了大量抽象简化。但一旦对结构作几何和拓扑改变,网格自动划分就变得极为困难。这就是几十年来,CAE/CAD 一体化研究,尽管有实力雄厚的国际大公司的大量人力财力投入,至今没有真正实现的原因。另外,有限元方程是对原控制微分方程的一种近似(弱形式),有限元法得到的解不满足原微分方程。所以其精度,特别是结构危险部位的应力精度,通常不能令人满意。边界积分方程则与原微分方程完全等价,而且对试函数的连续性要求比有限元法还要低。边界积分方程的基本解其实就是物理定律在位势理论中的表达式。工程界人士也许不欣赏基本解的奇异性,但奇异性是所有物理定律的共同特性。如黑洞就是广义相对论方程的一个奇异解(由于爱丁顿不相信黑洞存在,以致钱德拉塞卡博士后出站时在英国找不到工作,然而三十年后他获得了诺贝尔奖)。所以正因为奇异的基本解存在,边界元法才可以称得上是科学方法。
相对于求解边值问题的三大类数值方法:有限差分法、有限元法和边界元法, 在佛教中也恰好有三乘佛法。将二者做一对比也许是有意思的。
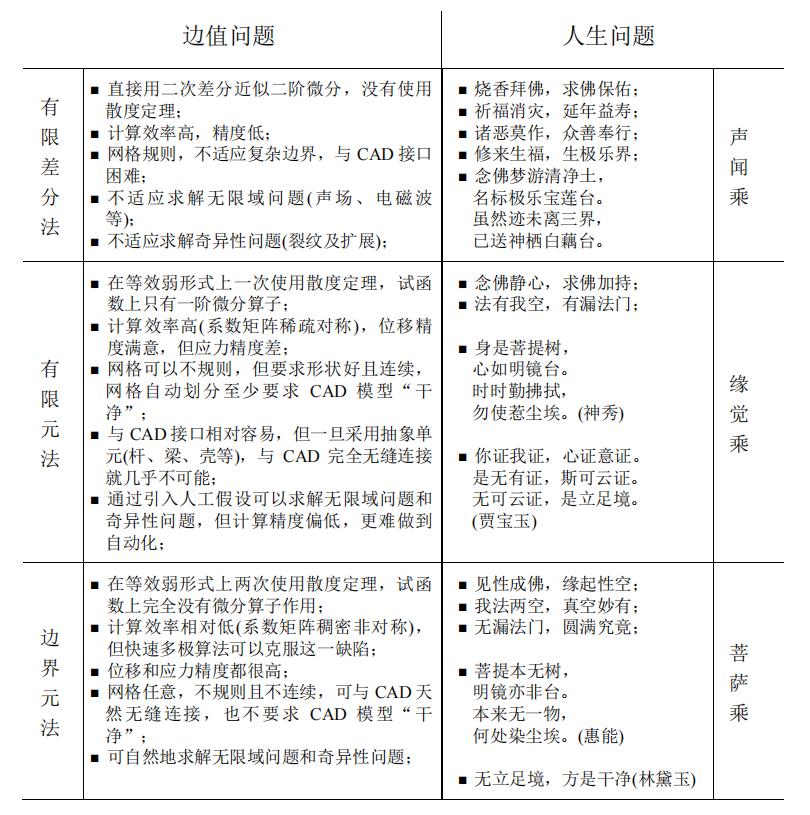 在上面的对比中关于三乘佛法境界的区分并不符合佛教界的传统标准,只是借用来说明边界积分方程方法是一个"圆满究竟的无漏法门"。然而,如此优雅完美的理论方法却没有产生一定规模的工程应用,如此迅速地到了"末法时代",面临着被边缘化的尴尬境地。每当我翻看杜先生编写的《边界积分方程方法——边界元法》,想到前贤们做了那么多精深优美的工作,难道这些工作就要被淹没被淘汰被遗忘?每念及此,心沉鼻酸。"孤标傲世偕谁隐,一样开花为底迟?"Heaviside 曾说"Logic can be patient for it is eternal"。我相信"边界积分方程可以等待,因为它是科学的"。当今世界,技术虽然日新月异,但基础理论几乎不变。所以基于科学方法开发的软件,必定经久不衰。
在上面的对比中关于三乘佛法境界的区分并不符合佛教界的传统标准,只是借用来说明边界积分方程方法是一个"圆满究竟的无漏法门"。然而,如此优雅完美的理论方法却没有产生一定规模的工程应用,如此迅速地到了"末法时代",面临着被边缘化的尴尬境地。每当我翻看杜先生编写的《边界积分方程方法——边界元法》,想到前贤们做了那么多精深优美的工作,难道这些工作就要被淹没被淘汰被遗忘?每念及此,心沉鼻酸。"孤标傲世偕谁隐,一样开花为底迟?"Heaviside 曾说"Logic can be patient for it is eternal"。我相信"边界积分方程可以等待,因为它是科学的"。当今世界,技术虽然日新月异,但基础理论几乎不变。所以基于科学方法开发的软件,必定经久不衰。边界积分方程理论(即高等数学里的第二格林公式)的提出,最早可追溯到19 世纪,比有限元理论早 100 多年。边界元法的研究也几乎与有限元法同时起步,两者并驾齐驱。有限元软件越做越大越强。而边界元软件,在初期虽有几家, 但不久都日渐式微,昙花一现。个中原因,我试想有以下几种:
(1) 早期计算机硬件不够发达,计算机资源十分有限,算法的效率和内存需求成为最突出的问题。
(2) 边界元法研究者没有认识到边界积分方程的本质优点,错误地以为其最大优点是降维(只划分表面网格)。对于非均质非线性问题,花费大量精力用在如何避免体积分上。虽然产生了一些数学形式上漂亮的工作,但最终都是徒劳。甚至在避免奇异积分方面也浪费了不少精力。
(3) 边界元法的软件实现,都是套用有限元法的网格,对结构的边界变量描述不完备,也不能逾越有限元法在 CAE/CAD 一体化过程中所面临的鸿沟。
现今边界元软件开发环境得到了极大改善。首先是计算机硬件已经发展到相当水平,足以适应基于不加简化的原始科学算法进行一定规模的计算。其次,也特别重要的是,快速算法的出现将边界元法的计算复杂度降低到线性或几乎线性量级。在强调自动化智能化的今天,针对有限元软件在 CAE/CAD 一体化中难以克服的困难,利用边界积分方程与生俱来的与 CAD 完全无缝连接的天然优势,开发一套CAD/CAE 天衣无缝的计算力学软件,应该是振兴边界元法的一个重要契机。"苍龙日暮还行雨,老树春深更著花"。十多年来,我在缺米愁柴的境况中,开始时夜以继日,后来身体不行了,也仍然不分节假日,一旦有了生存下去的条件,就潜心于程序中,心无旁骛。绕了九九八十一道弯,终于搭建成了一个完全融于 CAD 环境中的 CAE 分析软件框架。该软件框架全部用 C++编写,目前已有 90 个项目,近2000 个源文件,设计 4714 个类,共约 80 万句。在这个"举世纷纷宝鱼目,投人慎勿以明珠"的时代,凭一己之力,在短期内从最基础数据结构做起,开发一套与已经发展了几十年的商业有限元软件相抗衡的分析软件,谈何容易。其艰难心酸, 有几首歪诗为证:
十年辛苦不寻常,
此身难逃名利坊。
不寻天路攀玉桂,
单向荒蛮踏冰霜。
痴僧西天求圣法,
顽猴东海乞宝藏。
今日握得金箍棒,
莫复冷灶愁米粮。
心事总在程序中,
奋不顾身十年同。
算法亦有蓬莱景,
编程岂无鸦片功。
狷狂本是书生色,
疏愚不合世流丛。
早知前路非坦荡,
九转千回梦未空。
忙忙碌碌又十年,
劳苦赢得一身残。
冷色时见有肚咽,
热泪常流无风干。
人情可通青云路,
学问原来不值钱。
幸有编程可相伴,
频频忘却世间烦。
十年编程似远征,
风雨无阻费劳神。
难忍压力几度弃,
已无退路续前程。
麓山脚下见孤影,
湘水岸边遗泪痕。
敝履柴车一瘦客,
黄粱不是梦里人。
月月天天岁有十,
穷愁添得鬓边丝。
乖张不入时人眼,
落寞独吟陶令诗。
人间是非冤谁解,
胸中块垒苦自知。
烦恼皆因妄执起,
但向经书觅菩提。
与现有的商业有限元软件及边界元软件相比,这个软件框架是一个全新的计算力学软件平台。在研发过程中遇山钻洞遇堑搭桥,面对每一个过不去的坎,没有采用变通的办法绕过去,而是进行硬生生的攻坚战,将它们彻底征服。算法上尽量做到自然而科学,避免投机取巧和拼凑。新的主要算法有:
(1) 边界面法。将边界积分方程和计算机图形学结合起来,继承了边界元法的所有优点同时避免对结构作几何上的简化,直接在结构的三维实体模型上进行应力分析,是一种真正的等几何分析方法。
(2) 双层插值法。将单元插值与无网格法结合起来,统一了连续和不连续单元,同时还给边界积分方程的边界变量一个完备描述。双层插值法既可以插值非连续函数,也可以用不连续网格插值连续函数,使得变网格计算简单易行,因而适宜非线性问题。利用简单的二叉树网格生成算法产生非连续网格,可实现任意复杂结构的全自动 CAE 分析,彻底将 CAE 从网格划分的牢笼中解放出来。
(3) 自适应快速多极算法和自适应几何交叉近似算法。实现了分级矩阵的所有代数运算以及它们的 Out Of Core 算法(包括直接求逆和 LU 分解),使得边界积分方程在大规模问题上的应用不再是难题。
(4) 单元球面细分法。实现了对任意基本解类型、任意单元形状、任意源点位置的奇异、超奇异以及近奇异积分的任意精度计算。
该软件从原始 CAD 模型到 CAE 分析再到后处理全过程全自动,称之为5aCAE(详见 http://www.5aCAE.com)。用户不需要懂得计算力学专门知识,不需要选择单元类型,只需根据实际情况定义材料、荷载和边界约束即可。施加约束和载荷也是在 CAD 的环境中完成,且都是具体直观地施加在几何体上。
我以为继承和发扬杜先生开创的事业,是纪念先生最好的方式。下面用一首七律纪念杜先生,并以之结束本文。
仿真原本万年计,
廿载毋论百年功。
振臂一声开新域,
摇旗几度聚旧朋。
多极运筹远近别,
双层插值断连同。
先生有灵应喜甚,
边元振兴绍宗风。